Виртуальный кабинет информатики и ИКТ Горловского лицея № 88 "Мечта"
menu

Урок 19. Основные алгоритмические конструкции. Ветвление. Неполная форма ветвления

Основные алгоритмические конструкции

Ключевые слова: 

• следование 
• ветвление 
• повторение 
• линейные алгоритмы 
• разветвляющиеся алгоритмы 
• циклические алгоритмы 

Человеку в жизни приходится решать множество различных задач. Решение каждой из них описывается своим алгоритмом, и разнообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения. Это положение выдвинул и доказал Э. Дейкстра в 70-х гг. прошлого века.

 

Эдсгер Вибе Дейкстра (1930-2002) — выдающийся нидерландский учёный, идеи которого оказали огромное влияние на развитие компьютерной индустрии.

2.4.2. Ветвление

 Ветвление — алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей). Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.

Блок-схема ветвления представлена на рис. 2.9. Каждая ветвь может быть любой степени сложности (рис. 2.9, а), а может вообще не содержать предписаний (рис. 2.9, б).

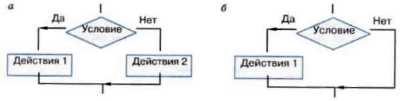
Рис. 2.9. Структура «ветвление»: а — полная форма ветвления; б — неполная форма ветвления

 

На алгоритмическом языке команда ветвления записывается так:

Для записи условий, в зависимости от результатов проверки которых выбирается та или иная последовательность действий, используются операции сравнения:

А<B — А меньше В; 
А<=В — А меньше или равно В; 
А=B — А равно В; 
А>В — А больше В; 
А>=В — А больше или равно В; 
А<>B — А не равно В.

Здесь буквы А и В можно заменять на любые переменные, числа и арифметические выражения. Приведённые операции сравнения допускаются и для символьных переменных.

Пример 7. Алгоритм вычисления функции f(x) = |x| для произвольного числа х.

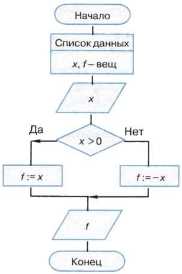
Обратите внимание на второй блок этой блок-схемы. В нём представлены имена и типы величин (данных), обрабатываемых в алгоритме.

Условия, состоящие из одной операции сравнения, называются простыми. В качестве условий при организации ветвлений можно использовать и составные условия. Составные условия получаются из простых с помощью логических связок and (и), or (или), not (не): and означает одновременное выполнение всех условий, or — выполнение хотя бы одного условия, a not означает отрицание условия, записанного за словом not.

Пример 8. Алгоритм определения принадлежности точки х отрезку [а, b]. Если точка х принадлежит данному отрезку, то выводится ответ ДА, в противном случае — НЕТ.

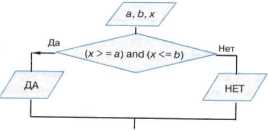
 Существует достаточно много ситуаций, в которых приходится выбирать не из двух, а из трёх и более вариантов. Есть разные способы построения соответствующих алгоритмов. Один из них — составить комбинацию из нескольких ветвлений.

Пример 9. Алгоритм, в котором переменной У присваивается значение большей из трёх величин А, В и С.

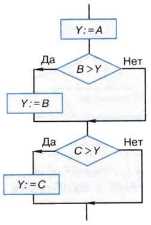
Пусть А = 10, В = 30 и С = 20. Тогда процесс выполнения алгоритма можно представить в следующей таблице:

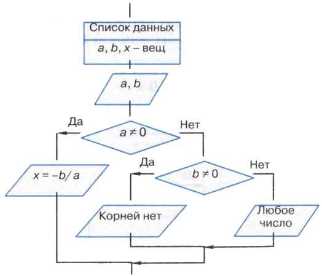
Пример 10. Алгоритм решения линейного уравнения ax + b = 0.

Пример 11. Исполнитель Робот может выполнять ту или иную последовательность действий в зависимости от выполнения следующих простых условий:

Также Робот может действовать в зависимости от выполнения составных условий.

Подумайте, в какую клетку переместится Робот из клетки, обозначенной звёздочкой, при выполнении следующего фрагмента алгоритма.

 

Ознакомьтесь с размещённым в Единой коллекции цифровых образовательных ресурсов модулем для коллективной работы «Алгоритмы с ветвящейся структурой» (217044). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.

 

Вопросы и задания

11. Какие алгоритмы называют разветвляющимися?

12. Приведите пример разветвляющегося алгоритма:

а) из повседневной жизни; 
б) из литературного произведения; 
в) из любой предметной области, изучаемой в школе.

13. Дополните алгоритм из примера 9 так, чтобы с его помощью можно было найти наибольшую из четырёх величин А, В, С и D.

14. Составьте алгоритм, с помощью которого можно определить, существует ли треугольник с длинами сторон а, b, с.

15. Составьте алгоритм, с помощью которого можно определить, является ли треугольник с заданными длинами сторон а, b, с равносторонним.

16. Составьте алгоритм возведения чётного числа в квадрат, а нечётного — в куб.

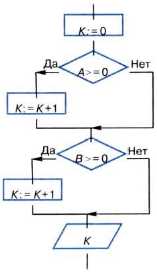
17. Какая задача решается с помощью следующего алгоритма?

18. Составьте блок-схему алгоритма определения количества чётных чисел среди заданных целых чисел А, Б и С.

19. Составьте блок-схему алгоритма определения принадлежности точки X отрезку [А, B] (пример 8) с использованием комбинации из двух ветвлений.

20. Составьте блок-схему алгоритма правописания приставок, оканчивающихся на букву "з".

21. Известно, что 31 января 2011 года было понедельником. Какие значения должны быть присвоены литерной переменной у в алгоритме, определяющем день недели для произвольного числа (chislo) января 2011 года?

22. Даны две точки на плоскости. Определите, какая из них находится ближе к началу координат.

23. Определите, есть ли среди цифр заданного целого трёхзначного числа одинаковые.

Электронное приложение к уроку

liniya 

   
  Презентации, плакаты, текстовые файлы Вернуться к материалам урока Ресурсы ЭОР  

 

liniya 

Cкачать материалы урока

 Презентация «Основные алгоритмические конструкции. Ветвление»

 Презентация «Основные алгоритмические конструкции. Ветвление» (Open Document Format)

Ссылки на ресурсы ЕК ЦОР

Свободное программное обеспечение: