Урок 4. Восьмеричная и шестнадцатеричные системы счисления. Компьютерные системы счисления
Восьмеричная система счисления
 Восьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
Восьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
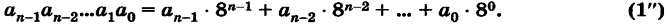
Например: 10638 = 1 • 83 + 0 • 82 + 6 • 81 + 3 • 80 = 56310.
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.
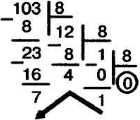
10310 = 1478
Шестнадцатеричная система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,..., 9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3AF16 означает:
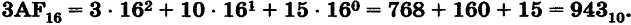
Пример 7. Переведём десятичное число 154 в шестнадцатеричную систему счисления.
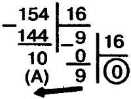
15410 = 9А16
![]() Презентация «Системы счисления»
Презентация «Системы счисления»
![]() Презентация «Системы счисления» (Open Document Format)
Презентация «Системы счисления» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
- анимация «Непозиционные системы счисления» (134984);
http://school-collection.edu.ru/catalog/res/6325be41-69cd-4980-8e51-7e6f5c526d65/?inter - демонстрация к лекции «Развернутая форма записи числа» (128629);
http://school-collection.edu.ru/catalog/res/a96df437-5ae3-4cab-8c5f-8d4cd78c5775/?inter - анимация «Преобразование десятичного числа в другую систему счисления» (135050);
http://school-collection.edu.ru/catalog/res/b6f80d82-fc7d-49de-943b-6082c2ab31f8/?inter - анимация «Сложение и вычитание одноразрядных двоичных чисел» (128618);
http://school-collection.edu.ru/catalog/res/8bb7eefa-4ed9-43fe-aebe-4d6ac67bc6ec/?inter - анимация «Сложение и вычитание многоразрядных двоичных чисел» (128624);
http://school-collection.edu.ru/catalog/res/67cbf74b-f85a-4e9d-88c5-58f203fb90ce/?inter - анимация «Умножение и деление двоичных чисел» (128634);
http://school-collection.edu.ru/catalog/res/caeea6cc-bd1d-4f47-9046-1434ac57e111/?inter - виртуальная лаборатория «Цифровые весы» (135009);
http://school-collection.edu.ru/catalog/res/498254ee-208d-4f10-96ff-192e79e2d25b/?inter - анимация «Арифметические операции в позиционных системах счисления» (128623);
http://school-collection.edu.ru/catalog/res/58ada0e5-fc12-42b1-9978-7a583b483569/?inter - анимация «Преобразование чисел между системами счисления 2, 8, 16» (135020);
http://school-collection.edu.ru/catalog/res/21854672-a155-4879-b433-bae02a2d1bd8/?inter - анимация «Схема Горнера» (134855);
http://school-collection.edu.ru/catalog/res/2fdc33fd-27d9-477c-9cbb-0a26d056af03/?inter - анимация «Перевод десятичных чисел в другие системы счисления» (128625);
http://school-collection.edu.ru/catalog/res/78ba290c-0f7c-4067-aaf4-d72f40f49f3b/?inter - анимация «Перевод недесятичных чисел в десятичную систему счисления» (128615);
http://school-collection.edu.ru/catalog/res/1a264912-eca9-4b45-8d77-c3655b199113/?inter - интерактивный задачник, раздел «Системы счисления» (128659).
http://school-collection.edu.ru/catalog/res/fc77f535-0c00-4871-b67c-fa2ecf567d46/?inter
Федеральный центр информационных образовательных ресурсов:
- информационный модуль «Понятие о системах счисления»;
http://fcior.edu.ru/card/1610/ponyatie-o-sistemah-schisleniya.html - контрольный модуль «Понятие о системах счисления»;
http://fcior.edu.ru/card/2770/ponyatie-o-sistemah-schisleniya.html - информационный модуль «Представление числовой информации с помощью систем счисления. Алфавит, базис, основание. Свернутая и развернутая форма представления чисел»;
http://fcior.edu.ru/card/11636/predstavlenie-chislovoy-informacii-s-pomoshchyu-sistem-schisleniya-alfavit-bazis-osnovanie-svernutaya-i-razvernutaya-forma-predstavleniya-chisel.html - контрольный модуль «Представление числовой информации с помощью систем счисления. Алфавит, базис, основание. Свернутая и развернутая форма представления чисел»;
http://fcior.edu.ru/card/6815/predstavlenie-chislovoy-informacii-s-pomoshchyu-sistem-schisleniya-alfavit-bazis-osnovanie-svernutaya-i-razvernutaya-forma-predstavleniya-chisel.html