Виртуальный кабинет информатики и ИКТ Горловского лицея № 88 "Мечта"
menu

Урок 8. Элементы алгебры логики. Высказывание. Логические операции

Элементы алгебры логики

Ключевые слова:

  • алгебра логики
  • высказывание
  • логическая операция
  • конъюнкция
  • дизъюнкция
  • отрицание
  • логическое выражение
  • таблица истинности
  • законы логики

1.3.1. Высказывание

 Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.

Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.

 Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six Is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.

В русском языке высказывания выражаются повествовательными предложениями. Но не всякое повествовательное предложение является высказыванием.

Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.

Относительно предложения «Компьютерная графика — самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.

Побудительные и вопросительные предложения высказываниями не являются.

Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл?».

Высказывания могут строиться с использованием знаков различных формальных языков — математики, физики, химии и т. п.

Примерами высказываний могут служить:

  1. «Na — металл» (истинное высказывание);
  2. «Второй закон Ньютона выражается формулой F=m•а» (истинное высказывание);
  3. «Периметр прямоугольника с длинами сторон a и b равен а • b» (ложное высказывание).

Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:

  1. «3 + 5 = 2 • 4» (истинное высказывание);
  2. «II + VI > VIII» (ложное высказывание).

Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X < 12» становится высказыванием только при замене переменной каким-либо конкретным значением: «5 < 12» — истинное высказывание; «12 < 12» — ложное высказывание.

Обоснование истинности или ложности высказываний решается теми науками, к сфере которых они относятся. Алгебра логики отвлекается от смысловой содержательности высказываний. Её интересует только то, истинно или ложно данное высказывание. В алгебре логики высказывания обозначают буквами и называют логическими переменными. При этом если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно — нулём (Б = 0). 0 и 1, обозначающие значения логических переменных, называются логическими значениями.

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.

Оперируя логическими переменными, которые могут быть равны только 0 или 1, алгебра логики позволяет свести обработку информации к операциям с двоичными данными. Именно аппарат алгебры логики положен в основу компьютерных устройств хранения и обработки информации. С применением элементов алгебры логики вы будете встречаться и во многих других разделах информатики. 

1.3.2. Логические операции

Высказывания бывают простые и сложные. Высказывание называется простым, если никакая его часть сама не является высказыванием. Сложные (составные) высказывания строятся из простых с помощью логических операций.

Рассмотрим основные логические операции, определённые над высказываниями. Все они соответствуют связкам, употребляемым в естественном языке.

 

Конъюнкция 

Рассмотрим два высказывания: А = «Основоположником алгебры логики является Джордж Буль», В = «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике». Очевидно, новое высказывание «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике» истинно только в том случае, когда одновременно истинны оба исходных высказывания.

Самостоятельно установите истинность или ложность трёх рассмотренных высказываний.

Конъюнкция — логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Для записи конъюнкции используются следующие знаки: ∧, •, И, &. Например: А ∧ В, А • В, А И В, А & Б.

Конъюнкцию можно описать в виде таблицы, которую называют таблицей истинности:

В таблице истинности перечисляются все возможные значения исходных высказываний (столбцы А и В), причём соответствующие им двоичные числа, как правило, располагают в порядке возрастания: 00, 01, 10, 11. В последнем столбце записан результат выполнения логической операции для соответствующих операндов.

Иначе конъюнкцию называют логическим умножением. Подумайте почему. 

Дизъюнкция 

Рассмотрим два высказывания: А = «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», В = «Лейбниц является основоположником бинарной арифметики». Очевидно, новое высказывание «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу или Лейбниц является основоположником бинарной арифметики» ложно только в том случае, когда одновременно ложны оба исходных высказывания.

Самостоятельно установите истинность или ложность трёх рассмотренных высказываний.

Дизъюнкция — логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Для записи дизъюнкции используются следующие знаки: ∨, |, ИЛИ, +. Например: A∨B, А|В, А ИЛИ Б, А+Б.

Дизъюнкция определяется следующей таблицей истинности:

Иначе дизъюнкцию называют логическим сложением. Подумайте почему. 

Инверсия 

Инверсия — логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Для записи инверсии используются следующие знаки: НЕ, ¬, ‾. Например: НЕ А, ¬А, 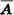А.

Инверсия определяется следующей таблицей истинности:

Инверсию иначе называют логическим отрицанием.

Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, «У меня дома нет компьютера». Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке одно и то же, «Я знаю китайский язык». Отрицанием высказывания «Все юноши 9-х классов — отличники» является высказывание «Неверно, что все юноши 9-х классов — отличники», другими словами, «Не все юноши 9-х классов — отличники».

Таким образом, при построении отрицания к простому высказыванию либо используется речевой оборот «неверно, что ...», либо отрицание строится к сказуемому, тогда к соответствующему глаголу добавляется частица «не».

Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логическом выражении выполняются в следующей очерёдности: инверсия, конъюнкция, дизъюнкция. Изменить порядок выполнения операций можно с помощью расстановки скобок.

Логические операции имеют следующий приоритет: инверсия, конъюнкция, дизъюнкция.

Пример 1. Пусть А = «На Web-странице встречается слово "крейсер"», В = «На Web-странице встречается слово "линкор"». Рассматривается некоторый сегмент сети Интернет, содержащий 5 000 000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В — для 4500 страниц, а высказывание A v В — для 7000 страниц. Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание?

а) НЕ (А ИЛИ В);

б) А & В;

в) На Web-странице встречается слово "крейсер" и не встречается слово " линкор".

Решение. Изобразим множество всех Web-страниц рассматриваемого сектора сети Интернет кругом, внутри которого разместим два круга: одному из них соответствует множество Web-страниц, где истинно высказывание А, второму — где истинно высказывание В (рис. 1.3).

Рис. 1.3.
Графическое изображение множеств Web-страниц

Изобразим графически множества Web-страниц, для которых истинны выражения и высказывание а) - в) (рис. 1.4)

Рис. 1.4.
Графическое изображение множеств Web-страниц, для которых истинны выражения и высказывание а) - в)

Построенные схемы помогут нам ответить на вопросы, содержащиеся в задании.

Выражение А ИЛИ В истинно для 7000 Web-страниц, а всего страниц 5 000 000. Следовательно, выражение А ИЛИ В ложно для 4 993 000 Web-страниц. Иначе говоря, для 4 993 000 Web-страниц истинно выражение НЕ (А ИЛИ В).

Выражение A ∨ B истинно для тех Web-страниц, где истинно А (4800), а также тех Web-страниц, где истинно В (4500). Если бы все Web-страницы были различны, то выражение A v В было бы истинно для 9300 (4800 + 4500) Web-страниц. Но, согласно условию, таких Web-страниц всего 7000. Это значит, что на 2300 (9300 - 7000) Web-страницах встречаются оба слова одновременно. Следовательно, выражение А & В истинно для 2300 Web-страниц.

Чтобы выяснить, для скольких Web-страниц истинно высказывание А и одновременно ложно высказывание В, следует из 4800 вычесть 2300. Таким образом, высказывание «На Web-странице встречается слово "крейсер" И не встречается слово "линкор" » истинно на 2500 Web-страницах.

Самостоятельно запишите логическое выражение, соответствующее рассмотренному высказыванию.

На сайте Федерального центра информационно-образовательных ресурсов (http://fcoir.edu.ru/) размещён информационный модуль «Высказывание. Простые и сложные высказывания. Основные логические операции». Знакомство с этим ресурсом позволит вам расширить представления по изучаемой теме.

 

 Презентация «Элементы алгебры логики»

 Презентация «Элементы алгебры логики» (Open Document Format)

Ссылки на ресурсы ЕК ЦОР

Федеральный центр информационных образовательных ресурсов:

Свободное программное обеспечение:

 Элементы теории множеств