Виртуальный кабинет информатики и ИКТ Горловского лицея № 88 "Мечта"
menu

Урок 10. Элементы алгебры логики. Свойства логических операций

Свойства логических операций

Рассмотрим основные свойства (законы) алгебры логики.

При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.

Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

  1. Переместительный (коммутативный) закон

    А & В = В & А;

    A ∨ B = В ∨ А.

    • для логического умножения:
    • для логического сложения:
  2. Сочетательный (ассоциативный) закон

    (А & В) & С = А & (B & С);

    (A ∨ B) ∨ C = A ∨(B ∨ C).

    • для логического умножения:
    • для логического сложения:
  3. Распределительный (дистрибутивный) закон

    А & (В ∨ С) = (А & В) ∨ (А & С);

    A ∨ (B & С) = (A ∨ В) & (A ∨ С).

    • для логического умножения:
    • для логического сложения:
  4. Закон двойного отрицания

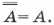
    Двойное отрицание исключает отрицание.

  5. Закон исключения третьего

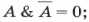
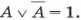
    • для логического умножения:
    • для логического сложения:
  6. Закон повторения

    А & А = А;

    A ∨ А = А.

    • для логического умножения:
    • для логического сложения:
  7. Законы операций с 0 и 1

    А & 0 = 0; А & 1 = А;

    A ∨ O = A; A ∨ l = l.

    • для логического умножения:
    • для логического сложения:
  8. Законы общей инверсии

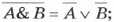
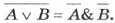
    • для логического умножения:
    • для логического сложения:

Законы алгебры логики могут быть доказаны с помощью таблиц истинности.

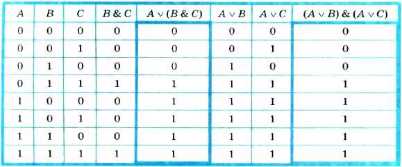
Докажем распределительный закон для логическического сложения:

A ∨ (В & С) = (А ∨ В) & (A ∨ С).

Совпадение столбцов, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.

Пример 2. Найдём значение логического выражения 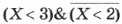 для числа Х = 0.

Решение. При X = 0 получаем следующее логическое выражение: 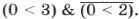. Так как логические выражения 0 < 3, 0 < 2 истинны, то, подставив их значения в логическое выражение, получаем: 1&Т = 1&0 = 0. 

 Презентация «Элементы алгебры логики»

 Презентация «Элементы алгебры логики» (Open Document Format)

Ссылки на ресурсы ЕК ЦОР

Федеральный центр информационных образовательных ресурсов:

Свободное программное обеспечение:

 Элементы теории множеств